The Mathematics of Skydiving

The Spread Stable position

1(a)y=mx+b (the equation of a linear equation)
Terminal Velocity of -53 m/s (falling so negative)
Free Fall begins at an altitude of 3000 meters

The equation would be:
y=-53x+3000

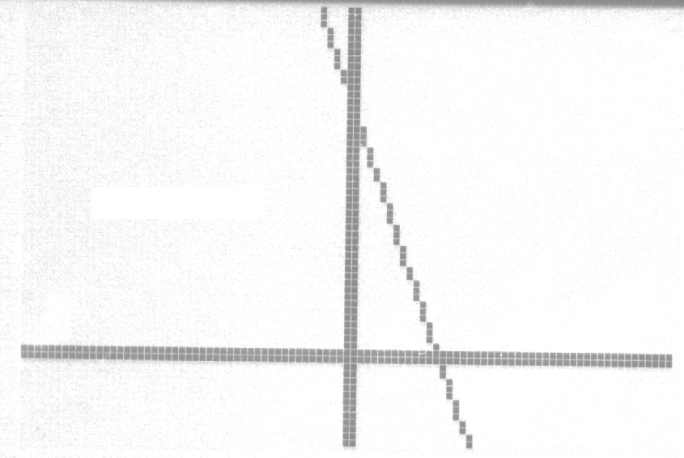
The graph of this line would look like the following:

(This picture was scanned directly from my TI-83 Plus calculator. Handy little device isn't it?)

(b) y=760

The graph of this line would look like the following:

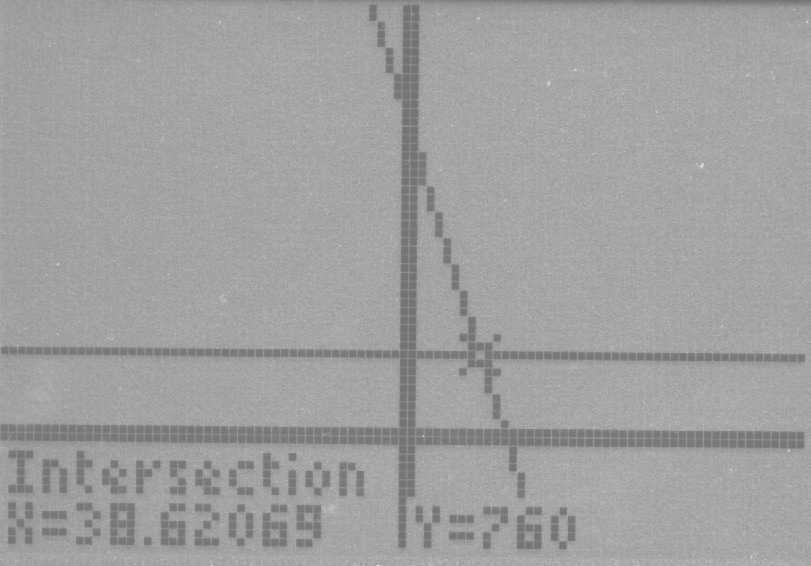
This line represents the minimum altitude a skydiver must deploy his or her parachute to ensure a safe deployment of their parachute.

(c) The intersection point is:

(42.3, 760)

This point represents the time and altitude the skydiver must deploy his or her parachute while in the spread stable position to ensure a safe deployment.

The point is shown on this graph:

(d) x values of the intersection point - y intercept
(0, 3000) = y intercept
(42.3, 760) = Intersection point
42.3-0=42.3
Free fall time is 42.3 seconds

2(a)descent velocity of 4 m/s
The distance the diver is above the ground is given by y=-4x+b
 I choose 1300 to be my value for b 
My new equation will be y=-4x+1300

The graph would look like:

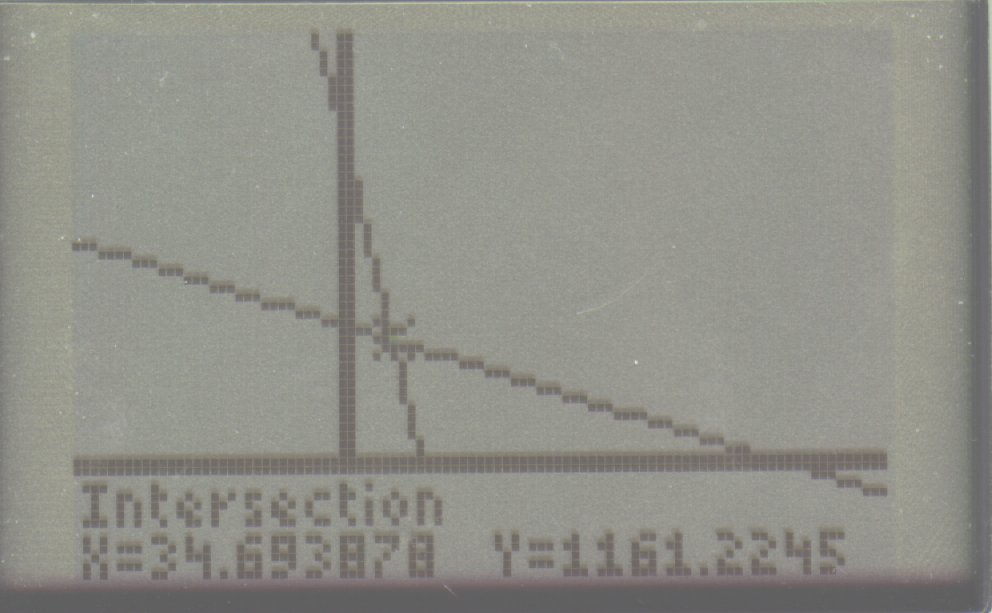
(b) I experimented with many values for example, 1500, 1200, and 1300

I decided to choose 1300 just because it was between those and it seemed to be the most logical at the time. 

(c) Intersection point of -4x+1300 and -53x+3000 is (34.7, 1161.2)
    y intercept (0, 1300)

The diver would fall at Terminal Velocity for 34.7 seconds.
 

(d) The height at which the skydiver deployed his parachute was 1161.2 meters.

(e) The x intercept is:

0     =   -4x+1300
-1300         -1300
-1300=-4x
-1300/-4

x=325
The x intercept minus the intersection point equals how long it takes the diver to reach the ground once the parachute is opened
325-34.7= 290.3

It would take 290.3 seconds to reach the ground once the diver has deployed his or her parachute.

1(a)y=mx+b (the equation of a linear equation)

The graph would look like this:

(b) y=760

The graph of this line would look like this:

This line represents the minimum altitude the skydiver must deploy his or her parachute for a safe deployment.

(c) The intersection point is:
(38.6, 760)

This point represents the time and altitude the skydiver must deploy his or her parachute while in the dive position to ensure a safe deployment. 
This point is shown on the graph

(d) x values of the intersection point - y intercept
y intercept is (0, 3000)
intersection point is (38.6, 760)
intersection point minus the y intercept equals free fall time
38.6-0=38.6

Free fall time in the dive position is 31.4 seconds.

2(a)descent velocity of 4 m/s
The distance the diver is above the ground is given by y=-4x+b
 I choose 1300 to be my value for b 
My new equation will be y=-4x+1300

The graph would look like:

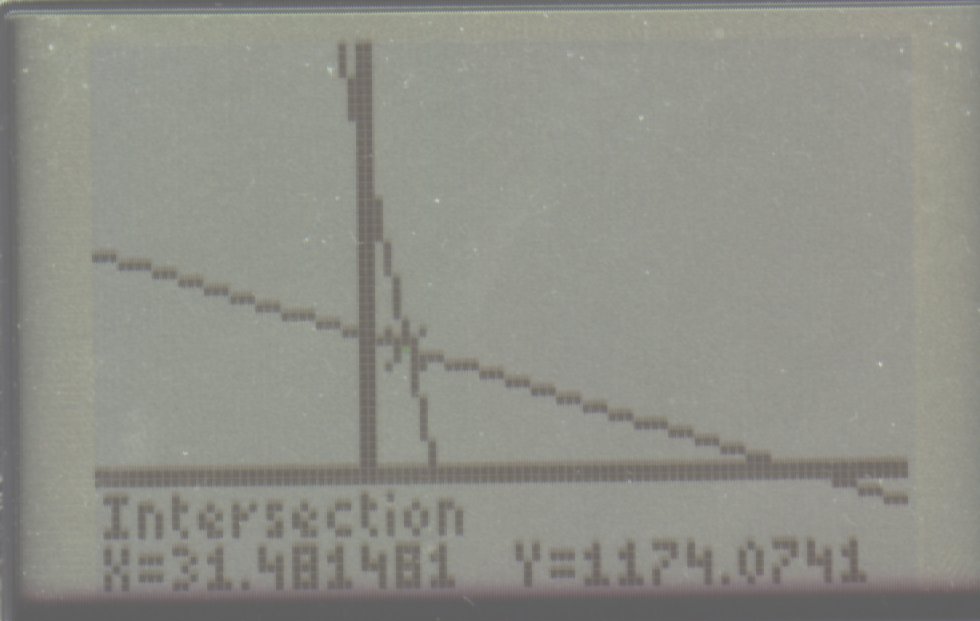
(b) I experimented with many values for b but I decided on 1300. The other values I tried were 1500, and 1200.

I decided to choose 1300 because I felt that it seemed to be the most logical line comparing to the others.

(c) Intersection point (31.5, 1174.0)
    y intercept (0, 1300)

intersection point - y intercept = how long the diver falls at Terminal Velocity
31.5-0= 31.5
The diver falls at Terminal Velocity for 31.5 seconds.
 

(d) The height at which the skydiver deployed his parachute was 1174.0 meters.

(e) The x intercept is:

0     =   -4x+1300
-1300         -1300
-1300=-4x
-1300/-4

x=325
The x intercept minus the intersection point equals how long it takes the diver to reach the ground once the parachute is opened
325-31.5= 293.5

It would take 293.5 seconds to reach the ground once the diver has deployed his or her parachute.